
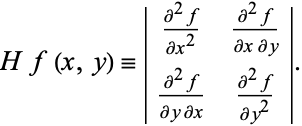
It is a weighted average of four coefficients. The y-iteration formula is far more interesting. The Runge-Kutta method iterates the x-values by simply adding a fixed step-size of h at each iteration. Predictor-corrector methods can be very much more efficient for problems where very high accuracy is a requirement. Generally speaking, high order does not always mean high accuracy. This will be superior to the midpoint method if at least twice as large a step is possible. The fourth-order Runge-Kutta method requires four evaluations of the right-hand side per step h. The fourth order Runge-Kutta method is based on computing y n+1 as follows A trade-off to perform several slope evaluations at each step and obtain a good accuracy makes the Runge-Kutta of order 4 the most popular.Īs usual, we consider an initial value problem \( y' = f(x,y), \quad y(x_0 )= y_0 \) and seek approximate values y k to the actual solution \( y= \phi (x) \) at mesh points \( x_n = x_0 + n\,h, \quad n=0,1,2,\ldots. However, there method may provide slightly different numerical answers due to round-off errors because they use different number of arithmetic operations. All Runge-Kutta algorithms of the same order m are equivalent from numerical analysis point of view as having the same accuracy. These methods can be constructed for any order m.

This idea was used moreĮach Runge-Kutta method is derived from an appropriate Taylor method in such a way that the final global error is of order O( h m), so it is of order m. Used extensively to obtain approximate solutions of differential equations
The fourth-order formula, known as the Runge-Kutta formula, has been Return to Part III of the course APMA0330 Return to the main page for the course APMA0340 Return to the main page for the course APMA0330 Return to Mathematica tutorial for the second course APMA0340

Return to Mathematica tutorial for the first course APMA0330 Return to computing page for the second course APMA0340 Return to computing page for the first course APMA0330 Laplace transform of discontinuous functions.Series solutions for the second order equations.Part IV: Second and Higher Order Differential Equations.Numerical solution using DSolve and NDSolve.Equations reducible to the separable equations.Wolfram Knowledgebase Curated computable knowledge powering Wolfram|Alpha. Wolfram Universal Deployment System Instant deployment across cloud, desktop, mobile, and more. Wolfram Data Framework Semantic framework for real-world data.


 0 kommentar(er)
0 kommentar(er)
